The Meaning of Life and Other Vegetables

Hello.

In my post two days ago, I started discussing Prof. Hoffman’s “Conscious Agents Universe” (an arbitrary name I made up for relating to it).

At this point, I’m going to take the liberty to tweak (or completely depart from) Hoffman’s theory. What I mean by that is that I’m not necessarily going to stick to his theory’s letter. Generally, I am committed to his ideas and I want whatever I say here to make consistent sense; but I’m not going to stick to every minor detail as he proposed it. Especially, when it comes to the mathematical model I will probably stray away from the original theory’s perspective (and maybe it will be significant, mathematically or otherwise). Please bear with me. I think my own take on this theory is still worthy of presentation, and I don’t want to have to do it while my hands (or mind) are firmly tied. Please still feel very welcome to point out significant deviations or apparent contradictions; that might trigger a valuable discussion regardless. Thank you, I appreciate the intellectual tolerance.

Today, I want to discuss the essence of the building blocks of the universe I’m discussing here. It might feel a little out of context at this point (especially if you haven’t read Hoffman’s The Case Against Reality), but I’d like to do it early on because laying down some base structures, in some detail, and coining some basic terminology, will come in handy later and allow a more flowing discussion of bigger ideas. I’ll try to go slow and develop the concept in stages.

So – the basic, indivisible (a-tom), irreducible building block is the Conscious Agent (CA). In the universe I’m discussing, everything conceivable is made up of CA (I am going to use “CA” for both singular and plural), and there is nothing else in existence. As an analogue, think of base particles in the physical world – for simplicity, you can think of atoms, though protons, electrons, neutrons, bosons, quarks and the likes might serve just as well. However, for discussion’s sake, let’s assume that the number of CA in existence is infinite.

I will refer to the the very basic CA as Elementary Conscious Agent (ECA). I’m mentioning it because CA can and do connect with each other to make exceedingly complex structures, which are also Conscious Agents. Confusing? I’ll get to that later.

So, what is an ECA, and how does it behave? What makes it “Conscious”? Loosely following Hoffman, the consciousness we are discussing here is the ability to respond to a stimulation non-automatically. The ECA receives a stimulation (just one channel, for simplicity), “makes a decision” how to respond, and outputs its response (again, single channel):

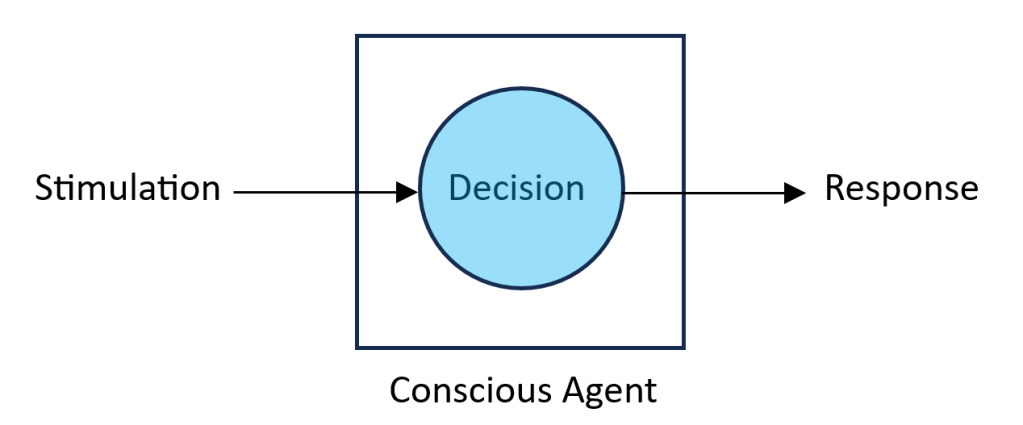
The above is a concise description of the CA. However, it’s a little crude for my purposes. At the next level of detail, the ECA would look like that:

As above, CA can connect and combine with each other to generate more complex entities – Complex Conscious Agents (CCA). Having given a little thought to it, I concluded that in order to be able to combine and generate enough variety to create intricate meaning, the ECA (or basic building block) would need to have at least 2 Inputs (Input A and Input B in the diagram above) and at least two outputs (Output X and Output Y). If it only had one input and one output (as in the first, conceptual diagram), all CA could do would be stringing together endlessly; and I am interested in a model that allows branching, looping back, and the likes. If there were more inputs than outputs (for example, two inputs and one output), or more outputs than inputs, the structures would be funneling in or out. An equal number seems (intuitively, at this stage) to allow maximum variety and flexibility in structuring and creating complexity. When I’m done laying out my case, you will see that allowing for maximum complexity is essential for this model.

The two inputs in the diagram above feed into a “processing black box”, which is where the decision is made. Then the response is output from that black box. At this level of abstraction it’s not critical how the decision is made. All that matters at this level is that we have input fed into a black box, a decision event, and an output that comes out the other side. This is the essence of the CA. At this level, both outputs are affected by both inputs, in a way that is unknown/unspecified.

As a side note, there is no “traditional” time notion in this model. Hoffman suggests that Spacetime is doomed (or already dead) – he explains why in his book; and that space and time, as we perceive them, are not fundamental to reality, but rather are aspects of “the interface” (which I’ll discuss more later). So, according to Hoffman there is no need for time in the model. there is, however, a sequence notion in his mathematical model; meaning that “steps” or “events” occur one after another. Among other things, this can give rise to causality. There is “before” and “after”, but durations (in the sense we are used to) are meaningless. It could be a nanosecond or a year between two subsequent “events”, and both would be equivalent. This is what I mean when I say, for example, “a decision event”. It only matters what came before it and after it, not “how long” something took.

Refining the model a little more, I suggest that the “decisions” are generated by probability functions:

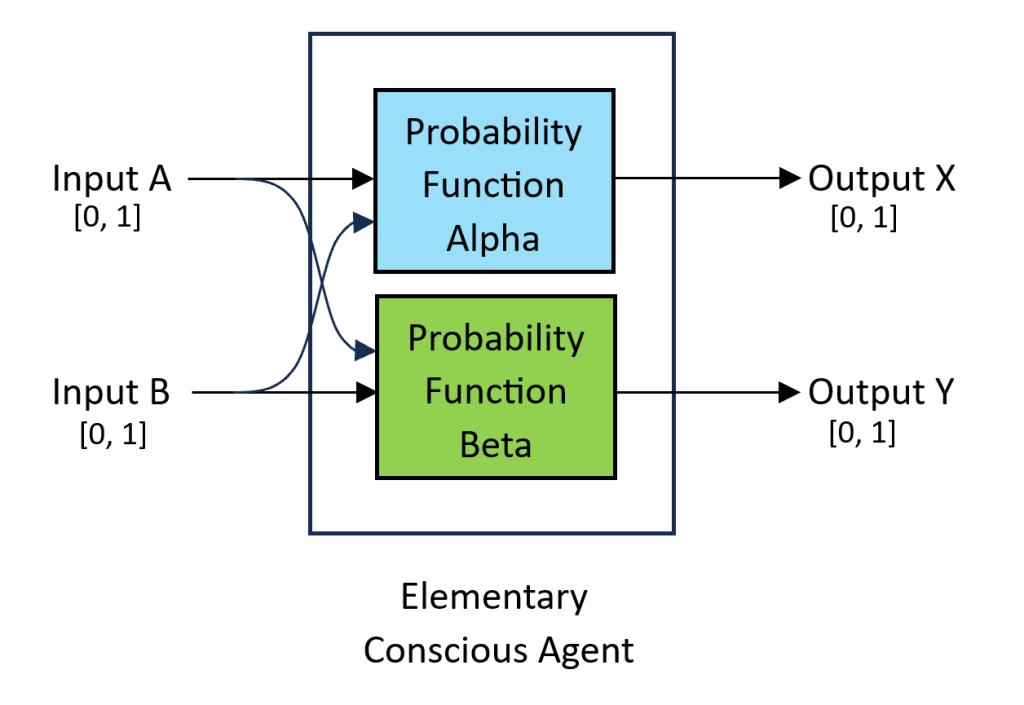
What this means it that the decisions (and outputs) are not deterministic; all that is set is the probabilities of the possible outcomes. To make the discussion more concrete, and to keep the model minimal, I decided that each channel (input or output) can only be either 0 or 1 (quiet or live).

An important aspect of the model suggested above is that each ECA has two separate probability functions. I tried to visualize that they can be completely different from each other, and operate independently. This is important for generating more variety in the population, and hence more potential complexity. Similarly, they can be different from one individual ECA to another.

Each probability function (or, in previous stages terms, decision-making black box) feeds a single output; but both inputs feed into each of the probability functions. This is somewhat arbitrary; I went with a gut feeling that this will promote variety and complexity (of both structure and behaviour), and at the same time will keep the basics simple enough for understanding and analyzing.

The last level of elaboration I intend to go into in today’s post deals with the internal workings of the probability functions:

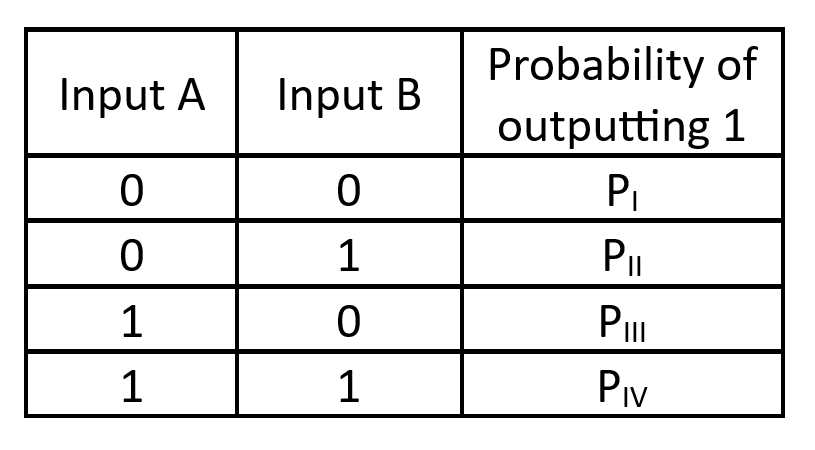
Each such probability function is a lookup table, that assigns, for any possible given input – {(0,0),(0,1),(1,0),(1,1)} a certain probability that it will trigger an output of 1, in the output channel associated with that specific probability function. For example, if P_II = 0.63 it means that when Input A is 0 and Input B is 1 there is a 63% chance that the output will be 1 (and a 37% chance that it will be 0). What will be the actual output (0 or 1) in any specific instance is unknown. Another way to describe it is, if that scenario was to be observed over, say, 10,000 independent occasions, about 6,300 of them would result in an output of 1, and about 3,700 in an output of 0.

The four P values in the above table can be any number between 0 and 1 (0-100%), and they can be different from each other, though there is nothing preventing two of them (or more) from being identical.

Incorporating the above into the ECA diagram provides the following result:

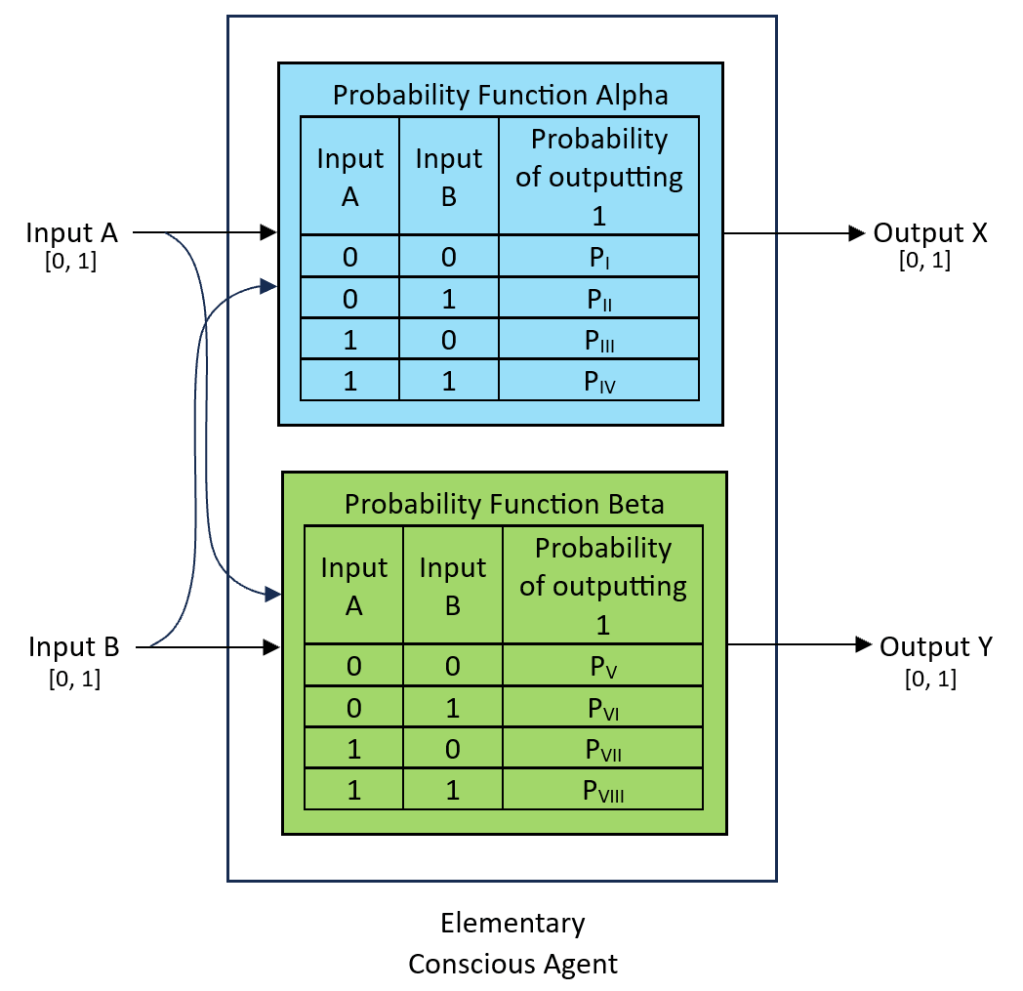
Again, please note that the values of P_I to P_VIII are independent of each other. They can be different (or the same) for probability functions Alpha and Beta, as well as among individual ECA.

This is all I wanted to present today; I feel it’s enough for one post. In following posts I will discuss other aspects of ECA and their behaviour, and speculate about the results of their characteristics, and how they relate to the universe and to us.

Peace to all.